differential equations and linear algebra pdf
- by stefanie
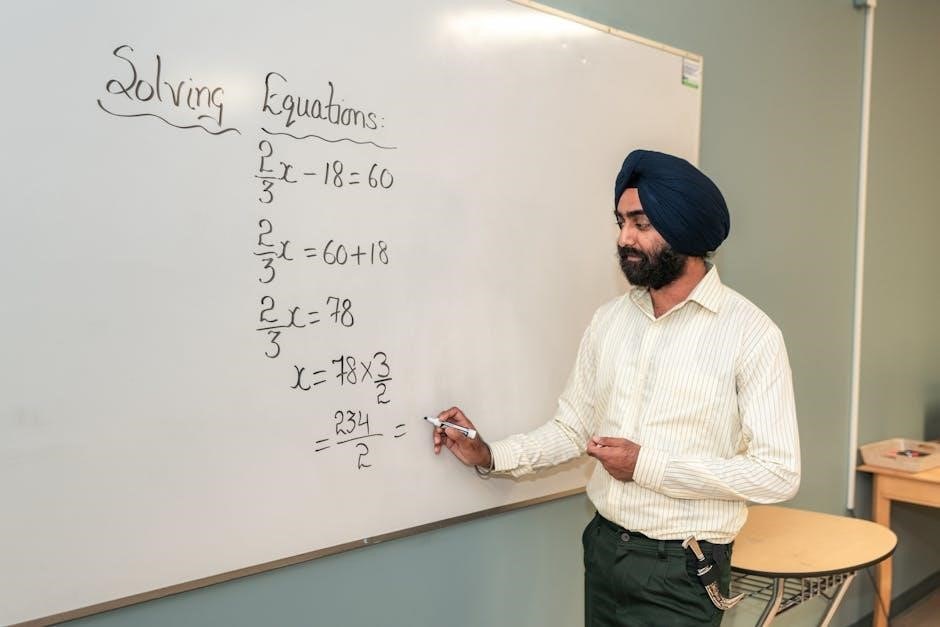
Differential equations and linear algebra are fundamental mathematical tools for modeling complex systems. Gilbert Strang’s resources provide a comprehensive introduction‚ blending theory and practical applications in engineering‚ physics‚ and beyond. This integrated approach simplifies understanding and problem-solving‚ making it essential for students and practitioners alike.
Overview of Differential Equations
Differential equations describe how quantities change over time or space‚ modeling dynamic systems in science and engineering. They are classified as ordinary (ODEs) or partial (PDEs)‚ depending on the variables involved. Linear equations‚ such as ( rac{dy}{dt} = y ) or ( rac{dy}{dt} = -y )‚ have constant coefficients and predictable solutions. Nonlinear equations‚ like ( rac{dy}{dt} = y^2 )‚ exhibit more complex behaviors. These equations are solved using analytical or numerical methods‚ with applications in growth models‚ physics‚ and engineering. Understanding differential equations is crucial for modeling real-world phenomena‚ from population growth to fluid dynamics.
Overview of Linear Algebra
Linear algebra is a core area of mathematics focusing on vector spaces‚ linear independence‚ matrices‚ and systems of linear equations. It provides essential tools for solving complex problems in engineering‚ physics‚ and computer science. Key concepts include linear combinations‚ determinants‚ and eigenvalues‚ which are vital for understanding system behaviors. Vector spaces define the framework for representing and manipulating data‚ while matrices offer a structured way to perform operations. Linear algebra is fundamental for solving systems of equations and analyzing dynamic systems‚ making it a cornerstone of modern applied mathematics and a crucial companion to differential equations in real-world applications.
Importance of Studying Both Subjects Together
Studying differential equations and linear algebra together is crucial for understanding their deep interconnections. Linear algebra provides essential tools‚ such as matrices and vector spaces‚ for solving differential equations. Eigenvalues and eigenvectors‚ central to both fields‚ simplify analyzing and solving complex systems. This integrated approach enhances problem-solving skills in engineering‚ physics‚ and data science. By combining these subjects‚ students gain a unified perspective‚ enabling them to model real-world phenomena effectively. The synergy between algebraic and differential methods fosters a deeper understanding of dynamic systems‚ making this dual study invaluable for modern scientific and engineering challenges.

Differential Equations
Differential equations describe how quantities change over time or space‚ appearing in growth models‚ physics‚ and engineering. They are classified as linear or nonlinear‚ with solutions providing insights into system behavior and dynamics.
Types of Differential Equations
Differential equations are broadly categorized into linear and nonlinear types. Linear equations‚ such as dy/dt = y or dy/dt = -y‚ have solutions that can be superimposed. Nonlinear equations‚ like dy/dt = y^2‚ exhibit more complex behavior. First-order equations involve a single derivative‚ while second-order equations include higher derivatives‚ such as d²y/dt² + y = 0. Systems of differential equations‚ like coupled equations‚ describe interactions between multiple variables. These classifications help determine appropriate analytical or numerical methods for solving them‚ making them essential tools in modeling real-world phenomena‚ from population growth to mechanical vibrations.
First-Order Differential Equations
First-order differential equations involve a single derivative of the dependent variable with respect to one independent variable. They are fundamental in modeling phenomena like population growth and heat transfer. These equations are classified into types such as separable‚ exact‚ and linear. Separable equations can be solved by isolating variables‚ while exact equations involve integrating factors. Linear first-order equations‚ such as dy/dt + P(t)y = Q(t)‚ are solved using integrating factors. Numerical methods‚ like Euler’s method‚ are also employed for complex cases. Understanding first-order equations is crucial as they form the basis for solving higher-order differential equations in various scientific applications.
Second-Order Differential Equations
Second-order differential equations involve the second derivative of the dependent variable and are commonly used to model oscillations‚ wave phenomena‚ and mechanical systems. These equations often arise in physics and engineering‚ such as in the study of simple harmonic motion or electrical circuits. They are typically linear and homogeneous‚ with constant coefficients‚ and their solutions depend on the roots of the characteristic equation. Real and distinct roots yield exponential solutions‚ while complex roots result in sinusoidal behavior. Understanding second-order equations is essential for analyzing dynamic systems‚ and their solutions often combine polynomial and exponential or trigonometric functions‚ making them versatile tools in scientific modeling.
Nonlinear Differential Equations
Nonlinear differential equations involve equations where the dependent variable or its derivatives are multiplied together or raised to higher powers‚ leading to complex behavior. Unlike linear equations‚ they do not follow the superposition principle‚ making them challenging to solve analytically. These equations often arise in real-world modeling‚ such as population dynamics‚ fluid flow‚ and electrical circuits. Numerical methods are frequently employed to approximate solutions‚ as exact solutions are rare. Nonlinear equations can exhibit phenomena like chaos‚ bifurcations‚ and oscillations‚ adding layers of complexity. Understanding nonlinear systems is crucial for accurately modeling natural processes‚ as they often better represent real-world scenarios compared to linear approximations.

Linear Algebra
Linear algebra focuses on vector spaces‚ matrices‚ and systems of linear equations. It provides essential tools for solving complex problems in science‚ engineering‚ and data analysis.
Systems of Linear Equations
Systems of linear equations are a cornerstone of linear algebra‚ involving equations where unknowns are multiplied by constants. These systems are solved using methods like Gaussian elimination or matrix inversion. They are fundamental in engineering‚ physics‚ and computer science for modeling real-world problems. Linear equations are defined by their linearity‚ ensuring no variables are squared or multiplied together. Solving such systems often involves matrices‚ determinants‚ and vector spaces‚ providing a structured approach to complex problems. Understanding these systems is essential for advancing in fields like machine learning and differential equations‚ where linear algebra serves as a foundational tool for analysis and computation.
Matrices and Determinants
Matrices and determinants are essential components of linear algebra‚ providing a structured way to organize and manipulate data. Matrices‚ as rectangular arrays of numbers‚ are fundamental in solving systems of linear equations and in various applications of differential equations. Determinants‚ calculated from square matrices‚ offer crucial information about the matrix’s invertibility and the system’s solvability. Understanding matrix operations‚ such as addition‚ multiplication‚ and inversion‚ is vital for advanced mathematical modeling. These concepts are not only foundational in engineering and physics but also in computer graphics and machine learning‚ where matrices play a central role in transformations and neural network algorithms‚ as highlighted in resources like Gilbert Strang’s textbooks and online courses.
Vector Spaces and Linear Independence
Vector spaces are foundational in linear algebra‚ representing collections of vectors that can be scaled and added together. Linear independence ensures that no vector in a set can be expressed as a combination of others‚ forming a basis for the space. Understanding these concepts is crucial for solving systems of equations and analyzing transformations. Orthogonal vectors in spaces like Rn simplify computations‚ while dimension theory provides insight into the space’s structure. These ideas are central to modern applications‚ from engineering to machine learning‚ where vector spaces model complex data and systems‚ as discussed in resources like Gilbert Strang’s textbooks and online courses.

Applications of Differential Equations and Linear Algebra
Differential equations and linear algebra are pivotal in engineering‚ physics‚ and real-world modeling. They solve systems in heat transfer‚ population dynamics‚ and economics‚ enabling precise problem-solving and forecasting.
Engineering Applications
Differential equations and linear algebra are indispensable in engineering for modeling dynamic systems. They are used to analyze heat transfer‚ fluid dynamics‚ and structural integrity. Linear algebra aids in solving systems of equations arising in circuit analysis and mechanical systems. Differential equations model population growth‚ economics‚ and signal processing. These tools enable engineers to forecast behavior‚ optimize designs‚ and solve complex problems efficiently. The combination of both subjects provides a robust framework for tackling real-world challenges‚ making them essential for modern engineering practices and innovations. Engineers rely on these mathematical foundations to develop solutions that are both accurate and scalable.

Physics and Dynamics
Differential equations are central to modeling physical phenomena‚ such as motion‚ heat transfer‚ and wave propagation. In dynamics‚ they describe how systems evolve over time‚ capturing Newton’s laws and oscillatory behaviors. Linear algebra complements this by providing tools for solving systems of equations that arise in physical models. Together‚ these disciplines enable physicists to analyze complex interactions‚ predict outcomes‚ and understand fundamental principles like energy conservation. From quantum mechanics to classical mechanics‚ differential equations and linear algebra form the mathematical backbone of physics‚ allowing for precise simulations and deeper insights into natural phenomena. Their integration is vital for advancing theoretical and applied physics research.
Real-World Modeling
Differential equations and linear algebra are indispensable for modeling real-world phenomena. They enable the mathematical representation of systems like population growth‚ financial markets‚ and disease spread. Differential equations capture how quantities change over time‚ while linear algebra provides tools for solving these equations in complex systems. Together‚ they allow for accurate predictions and simulations‚ essential for fields such as epidemiology‚ economics‚ and environmental science. By integrating these disciplines‚ professionals can develop robust models to analyze and forecast dynamic behaviors‚ aiding in decision-making and problem-solving across industries. This synergy is pivotal for addressing and understanding intricate‚ interconnected systems in the modern world‚ making them invaluable for practical applications.
Solving Differential Equations and Linear Systems
Analytical methods solve linear differential equations‚ while numerical techniques handle complex systems‚ supported by linear algebra for solving equation systems efficiently.
Analytical Methods for Linear Equations
Analytical methods for linear equations involve precise mathematical techniques to find exact solutions. These methods are fundamental in solving both differential equations and linear systems. For differential equations‚ techniques like separation of variables‚ integrating factors‚ and eigenvalue problems are commonly used. In linear algebra‚ methods such as Gaussian elimination and matrix inversion are applied to solve systems of equations. These approaches ensure accuracy and provide a deep understanding of the underlying mathematical structure. Analytical solutions are particularly valuable in engineering and physics‚ where precise modeling is critical. By mastering these methods‚ students gain the ability to solve a wide range of problems efficiently and effectively.
Numerical Methods for Complex Problems
Numerical methods are essential for solving complex problems in differential equations and linear algebra when analytical solutions are difficult or impossible to obtain. These methods discretize the equations‚ transforming them into manageable systems of linear equations. Techniques like finite differences‚ Runge-Kutta methods‚ and Gaussian elimination are widely used. Numerical approaches are particularly valuable for nonlinear differential equations and large-scale systems‚ where precision and efficiency are critical. They enable simulations and approximations that are indispensable in engineering‚ physics‚ and real-world modeling. By leveraging computational tools‚ numerical methods provide practical solutions to intricate mathematical problems‚ making them a cornerstone of modern scientific analysis and problem-solving.

Eigenvalues and Eigenvectors
Eigenvalues and eigenvectors are fundamental in linear algebra‚ essential for solving systems of equations and analyzing dynamics in differential equations. They determine system behavior and stability.
Theory and Computation
Eigenvalues and eigenvectors are foundational in linear algebra‚ with eigenvalues representing factors by which eigenvectors are stretched or compressed. Computationally‚ eigenvalues are found by solving the characteristic equation‚ while eigenvectors are derived through row reduction. The power iteration and QR algorithm are common methods for numerical computation. Gilbert Strang emphasizes their role in system stability and dynamics. Understanding eigenvalues is crucial for analyzing differential equations‚ as they determine system behavior‚ such as growth‚ decay‚ or oscillations. This duality between theory and computation makes eigenvalues and eigenvectors indispensable tools in both fields.
Applications in Differential Equations
Eigenvalues and eigenvectors play a pivotal role in solving and analyzing differential equations. They are essential for understanding system stability‚ where eigenvalues determine whether solutions grow‚ decay‚ or oscillate. In mechanical systems‚ eigenvalues help identify natural frequencies and vibration modes. Heat transfer problems utilize eigenvalues to model temperature distributions over time. Additionally‚ eigenvectors provide the shape of solutions‚ such as standing waves in physics or population dynamics in biology. These concepts bridge linear algebra and differential equations‚ offering powerful tools for modeling real-world phenomena like electrical circuits and fluid dynamics. Their applications are vast‚ making them indispensable in engineering and scientific problem-solving.
Differential equations and linear algebra are cornerstone subjects for problem-solving in science and engineering. For further learning‚ Gilbert Strang’s textbook and video series provide a robust foundation. Additional resources include online platforms like Chegg for step-by-step solutions and Professor Leonard’s tutorials on Patreon. Supplementary materials‚ such as problem sets from MIT OpenCourseWare‚ enhance understanding. These tools empower students to master mathematical modeling and analysis‚ essential for real-world applications in engineering‚ physics‚ and data science. Investing time in these resources will deepen comprehension and prepare learners for advanced challenges in their academic and professional journeys.
Related posts:
Unlock the essentials of differential equations and linear algebra with our free PDF guide. Perfect for students and professionals alike!
Posted in PDF